 ぱぱりん
ぱぱりん今日は、12月23日で関西統一日の1月14日まであと22日です。
今日から直前講習が始まります。
大晦日はもちろん、正月までびっしりと休みなく授業があります。
浜学園の直前講習については、別記事で詳しく書いていますので参照ください。


もうこの時期は、
ことだけに集中していってほしいと思います。
新しいことをやってもなかなか身につかないので、いままでやってきたことを取りこぼさず得点にする確認が大事になってきます。
その点に関して、浜学園の学園長からの受験生へのメッセージを参照ください。





すこし時間があったので、2022年の灘中と2023年の海陽中学特別給費の算数の過去問を眺めていました。
自分でも解けるかな?と思って解いてみました。
そこで、どちらの中学も似ている問題があることに気づきました。
それについて、私なりの解答を説明したいと思います。



問題のコツを知っていれば、簡単に解けると思います。
さっそく説明しますね。
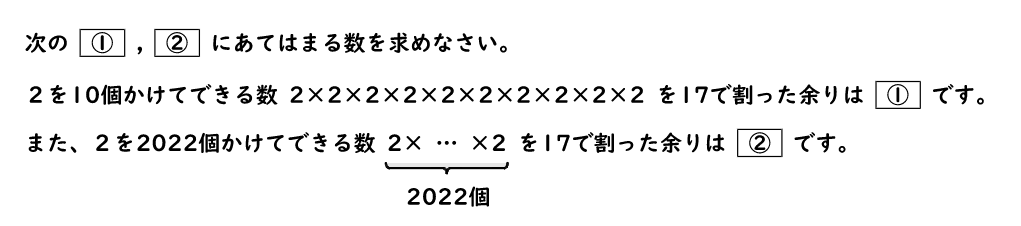




このような問題はパターンを見つければ一発で解けます。
超簡単な部類に入りますね。
まず、順番に考えていきます。
2を17で割ると余りは2
2×2を17で割ると余りは4
2×2×2を17で割ると余りは8
2×2×2×2を17で割ると余りは16
ここまでは簡単ですね。
2×2×2×2×2を17で割ると余りは「2の4乗を17で割った余り」である16×2を17で割ったあまりと同じなので15となります。



2の4乗は、17×1+16ですよね。
2の5乗は、2×(17×0+16)ということになるので、これを17で割った余りは、2×16の余りと同じになります。
その考え方を利用しながら進めていくと、
2の6乗を17で割った余りは、「2の5乗の余り」である15に2をかけて17で割った余りと同じなので、15×2÷17の余りだから13ということになります。
同様にして、
2の7乗を17で割った余りは、13×2÷17なので余りは9です。
2の8乗を17で割った余りは、9×2÷17なので余りは1です。



ポイントは余りが1となるときを見つけることです。
1が見つかると、それ以降は繰り返しになります。
すなわち、
2の9乗を17で割った余りは、1×2÷17なので余りは2です。
2の10乗を17で割った余りは、2×2÷17なので余りは4です。
以上のようになるので、余りを順番に並べると
2→4→8→16→15→13→9→1→2→4→8…
の繰り返しになるのです。
つまり「2,4,8,16,15,13,9,1」の8つの数字の繰り返しになります。
ですから、2の2022乗を17で割った余りは、
2022÷8をすると、252あまり6ですから、
「2,4,8,16,15,13,9,1」の8つの数字が252セットあり、
あまりが6ですから、6番目の「13」が答えとなります。



私でもノーヒントで解けるので簡単な部類だと思います。
もっと頭がいい子は、もっときれいにサクッと解けるようです。
つづいて、今年の海陽特別給費でも同じような問題が出たので見てみましょう。


これもパターンを見つけるだけです。
2023を23で割ると、あまりは22です。
2023×2023を23で割った余りは、「2023を23で割ったときのあまりである22」に22をかけて23で割った余りと同じですから、22×22÷23のあまり「1」ということになります。
つまり、2023×2023を計算するのは大変なので、あまり同士をかけた22×22をかけて23で割ったあまりを出せば、2023×2023を23で割ったあまりに一致するということです。



そして、もうポイントの1が出ちゃいましたね。
あまりで1が出ちゃうと楽勝です。
2023の1乗を23で割ると、あまりは22。
2023の2乗を23で割ると、あまりは1。
2023の3乗を23で割ると、あまりは22。
2024の4乗を23で割ると、あまりは1。
となり、奇数乗の余りは「22」、偶数乗の余りは「1」となるのです。



灘中学の過去問をやっていれば、秒殺できてしまう問題であったのではないでしょうか?
この手の問題は
「余りが1」となるところを見つけることで規則性を発見する
ことに尽きます。
いろんなやり方があるようですが、論理的に理解しやすいので子どもがわからなかったら上のように教えたいと思います。



逆にもっといい解き方があると言われそうですが。
帰ったら、長男と次男に問題を出してみたいと思います。
ちなみに、
7を2023回かけた一の位はいくらでしょうか?
というような問題が浜学園の2年生のテキストに載っていました。
7の2023乗したときの1の位を求めるということです。
実際に7を2023回かけるのは大変です。というか無理ですね。
ですからこれも法則を見つけることになります。
7を1回かけると一の位は「7」です。
7を2回かけると一の位は「9」です。
7を3回かけると一の位は「3」です。
7を4回かけると一の位は「1」になります。
ここでポイントは、
一の位だけに注目する
ということです。
ですから、十の位以上は完全に無視します。
それを頭に置いておくと、7を5回かけたときの一の位は、7を4回かけたときの一の位に7をかけただけでよいのです。
つまり、7を5回かけた時の一の位は、「1(7を4回かけたときの一の位)」に7をかけたものと同じになるので、「7」ということになります。
その法則を見つけると、7を6回かけた時の一の位は、「9」となります。
ということで、7→9→3→1→7→9→3→1→….の繰り返しになります。
以上より、7を2023回かけたときの一の位の値は、2023÷4=505あまり3なので、答えが3番目の「3」ということになります。



法則を見つければ簡単ですが、小学校2年生にはちょっと難しいですね。
さきほどの灘の問題は簡単ですが、ほかの問題はさすがに難しいのがたくさんですね。
特に小学生が解けるとは思えない場合の数の問題がえぐいです。
私自身、高校時代は数学が好きでそれなりに場合の数もたくさん解いてきましたが、灘の場合の数は難しいと思います。
これを小学生で解いてしまうんですから参りました。



灘中を目指すのであれば、算数の美しさを小学校から感じておかないと厳しいんだなということが改めてわかりました。
次男は、長男より上を目指したそうなので、いまから少しずつ目覚めていってくれればうれしいです。
長男からメールがあり、クラス分けは志望校の1組(4クラス中1番)だったとのことでした。
成績の報告メールっていうのは、いい時も悪い時もほぼないのですが、今回は最後のクラス分けとのことでうれしかったのかメールを送ってきたようです。
このままの勢いで本番まで駆け抜けてほしいです。
最後までお読みいただきありがとうございました。
皆様も一緒に合格できるよう頑張りましょう!











コメント